Cassinos Online no Brasil: Guia Completo para Escolher sua Experiência de Jogo
O Brasil está passando por mudanças significativas no setor de cassinos on-line. Elas refletem a evolução das atitudes em relação aos jogos de azar no país. Esse fenômeno faz parte de um contexto mais amplo de transformação social e tecnológica. Elas influenciaram as preferências de entretenimento da população brasileira.
A demanda por alternativas de lazer on-line tem crescido significativamente ao longo dos anos. Isso ocorreu devido à conectividade digital e à busca por entretenimento inovador. Em resposta a essa demanda, surgiram os cassinos online. Eles oferecem uma variedade de jogos de azar. Eles podem ser acessados por meio de dispositivos conectados à Internet.
Histórico legislativo dos jogos de azar no Brasil

A história legislativa dos jogos de azar no Brasil é complexa. Ela é caracterizada por várias fases. Elas incluem proibições e autorizações. Desde o início do século XX, houve mudanças significativas no país. Elas dizem respeito à regulamentação dos jogos de azar. Essas mudanças refletem as transformações culturais, sociais e econômicas.
No início do século XX, os cassinos eram parte integrante da vida social brasileira. Eles eram populares nas décadas de 1930 e 1940. Os cassinos eram legais e prosperavam. Na década de 1940, houve uma reviravolta na política de jogos de azar. Em 1946, o presidente Eurico Gaspar Dutra proibiu os cassinos.
A proibição rigorosa permaneceu em vigor por décadas. Nas últimas duas décadas, iniciou-se uma polêmica. Uma revisão dessa legislação está sendo considerada. Nas décadas de 1990 e 2000, houve tentativas de legalizar os cassinos. Essas tentativas foram acompanhadas de intenso debate.
Em 2018, ocorreu um fato importante. A Lei 13.756 foi aprovada. Ela autorizou a operação de apostas esportivas no Brasil. Isso se tornou um passo importante.
Atualmente, há um debate sobre a legalização abrangente dos jogos de azar. Isso inclui os cassinos on-line. Várias propostas foram apresentadas no Congresso. Isso demonstra uma mudança na percepção e no entendimento do papel dos jogos de azar na sociedade brasileira moderna.
A importância dos cassinos on-line na economia brasileira
Os cassinos on-line desempenham um papel importante na economia brasileira. O setor de cassinos on-line é um contribuinte notável para o desenvolvimento econômico do país.
Os cassinos on-line contribuem para a criação de empregos. Isso estimula a economia do Brasil. O setor de jogos de azar on-line está se expandindo. Isso abre oportunidades de trabalho em vários setores. Por exemplo, tecnologia, atendimento ao cliente, marketing e outros estão se desenvolvendo. As plataformas de cassino estão estimulando o crescimento e a inovação.
O apelo dos cassinos on-line também está se estendendo aos turistas internacionais. Isso está impulsionando o crescimento do setor de turismo no Brasil. Os visitantes são atraídos pelas plataformas de jogos de azar on-line. Eles podem explorar outros aspectos do país. Isso leva a um aumento nos gastos com turismo. As reservas de hotéis e a interação com empresas locais estão aumentando.
A regulamentação e a tributação dos cassinos on-line proporcionam um novo fluxo de receita para o governo brasileiro. A tributação das atividades de jogos de azar garante que uma parte dos lucros seja usada para desenvolver serviços públicos e infraestrutura. Isso aumentará ainda mais o bem-estar econômico geral do país.
O setor de cassinos on-line promove o avanço tecnológico e a inovação. Os cassinos on-line estão concentrados em oferecer a experiência de jogo mais avançada. Essas plataformas estão alimentando o crescimento tecnológico. Isso é evidente em áreas como realidade virtual, inteligência artificial e transações on-line seguras. Isso tem um impacto positivo no cenário tecnológico do Brasil como um todo.
Os cassinos online no Brasil impulsionam os gastos dos consumidores tanto no país quanto no exterior. Os jogadores participam do ciclo de movimentação econômica. Isso dá suporte às várias empresas envolvidas no ecossistema dos cassinos on-line. Esse aumento nos gastos pode levar a uma economia mais forte e dinâmica.
Os cassinos on-line têm um impacto social e cultural na sociedade brasileira. Eles oferecem uma nova forma de entretenimento e atividades de lazer. Isso influencia as escolhas de estilo de vida e as preferências de lazer.
A importância dos cassinos on-line para a economia brasileira é enorme. Ela vai além do setor de jogos de azar.
Jogos disponíveis nos cassinos on-line no Brasil

Os cassinos on-line no Brasil oferecem uma seleção de jogos emocionantes. Há jogos para todos os gostos. Eles atendem às preferências dos jogadores. Eles garantem uma experiência de jogo única para todos. Vamos dar uma olhada nos diferentes tipos de jogos disponíveis nos cassinos on-line do Brasil. Eles oferecem entretenimento empolgante aos jogadores.
- Caça-níqueis
Os caça-níqueis são a principal estrela dos cassinos on-line brasileiros. Os cassinos on-line têm uma variedade impressionante de temas. Há desde aventuras épicas até clássicos retrô. Esses jogos oferecem entretenimento fácil e emocionante. Basta selecionar suas linhas de pagamento, definir o tamanho da aposta e girar os rolos. Descubra emocionantes combinações vencedoras.
- Roleta on-line.
A roleta on-line é uma experiência de jogo clássica e empolgante. Há diferentes variações disponíveis. Por exemplo, a roleta americana e a roleta europeia. Elas permitem que os jogadores escolham sua favorita e apostem na sorte. A roleta on-line oferece emoção contínua.
- Blackjack on-line.
O blackjack é um dos jogos mais populares nos cassinos on-line. A estratégia é a chave para vencer o dealer e chegar a 21. Os jogadores podem explorar diversas variações. Isso torna cada mão única e desafiadora.
- Cassino ao vivo.
Para uma experiência autêntica, existem os cassinos ao vivo. Eles oferecem jogos com crupiês reais. Os jogadores podem jogar blackjack, roleta e outros jogos em mesas ao vivo. É possível interagir diretamente com os dealers. Isso está disponível no conforto de sua própria casa.
- Vídeo pôquer.
O vídeo pôquer está à disposição dos amantes do pôquer. É uma variação empolgante do clássico jogo de cartas. Os jogadores podem testar suas habilidades e ganhar prêmios incríveis.
- Raspadinhas.
As raspadinhas são um entretenimento rápido. Elas oferecem a oportunidade de ganhar prêmios instantâneos. Com uma variedade de opções, os jogadores podem experimentar a emoção das raspadinhas. Eles podem descobrir seus prêmios a qualquer momento.
- Esportes virtuais.
Os entusiastas de esportes podem apostar em esportes virtuais. Por exemplo, futebol e corrida de carros. Esses jogos trazem toda a emoção dos eventos esportivos para a tela. Eles proporcionam uma experiência única.
- Vídeo Bingo.
O vídeo bingo oferece uma experiência empolgante com variações temáticas exclusivas. Há variações como o bingo de 90 bolas. Aqui, os jogadores têm a chance de ganhar grandes jackpots. Eles podem desfrutar de uma atmosfera animada.
Estas são apenas algumas das opções de jogos disponíveis. A diversão nunca acaba aqui. As possibilidades são tão vastas quanto sua imaginação.
Fornecedores de jogos
Os cassinos online no Brasil cooperam com os principais fornecedores de jogos. Isso garante uma seleção variada e empolgante de jogos.
- Playtech. Esta é uma das maiores empresas do setor de jogos on-line. Ela domina os cassinos virtuais e ao vivo. As séries de jogos Kingdoms Rise e Age of the Gods oferecem grandes jackpots.
- Blueprint Gaming. Uma empresa do Reino Unido. É conhecida por criar jogos populares de caça-níqueis on-line. Por exemplo, Diamond Mines Megaways, Ted e The Goonies.
- NetEnt. Um desenvolvedor sueco que cria jogos inovadores. É especializada na criação de caça-níqueis, jogos de mesa e cassinos ao vivo. Starburst, Gonzo's Quest e Blood Suckers são alguns dos jogos mais populares da empresa.
- Microgaming. É um provedor de software. Foi agraciada com inúmeros prêmios. Oferece uma ampla gama de jogos inovadores. Por exemplo, Mega Moolah, Immortal Romance e Thunderstruck II.
- Pragmatic Play. Conhecida por seu portfólio diversificado de caça-níqueis de alta qualidade, cassino ao vivo e jogos de bingo. Desenvolveu Wolf Gold, Mustang Gold e Sweet Bonanza.
Esses renomados provedores oferecem aos jogadores do Brasil acesso a jogos de alta qualidade, inovação constante e entretenimento empolgante.
Métodos de pagamento em cassinos on-line no Brasil
Os cassinos online Brasil oferecem uma variedade de métodos de pagamento. Isso garante uma experiência de jogo fácil e segura. Os métodos de pagamento disponíveis são os seguintes:
|
Método de Pagamento |
Exemplo |
Descrição |
|
💳 Cartões de Crédito |
Visa, Mastercard |
Os cassinos on-line aceitam os principais cartões de crédito para transações rápidas e seguras. Depósitos instantâneos na sua conta do cassino. |
|
🏦 Transferência Bancária |
Banco do Brasil, Bradesco, Santander |
Opção confiável para depósitos e saques seguros. Transferências disponíveis para os bancos mais populares do Brasil. |
|
📄 Boleto Bancário |
Pagamento via boleto bancário |
Opção conveniente para quem prefere pagar em dinheiro. Gere o boleto no caixa eletrônico ou online e pague em qualquer banco autorizado. |
|
💼 Carteiras Digitais |
Neteller, Skrill |
Carteiras digitais populares para movimentar dinheiro online de forma rápida e segura. Ideais para depósitos e saques ágeis. |
|
🔐 Cartões Pré-pagos |
AstroPay Card |
Solução pré-paga para anonimato e segurança. Compre o cartão pré-pago e faça depósitos instantâneos em sua conta de cassino. |
Escolha o método de pagamento que melhor atenda às suas necessidades.
Bônus e promoções especiais para jogadores brasileiros
Os cassinos on-line no Brasil oferecem muitos bônus e promoções interessantes. Eles oferecem aos jogadores oportunidades incríveis. Eles podem ser usados para aprimorar a experiência de jogo.
- O bônus de boas-vindas.
Ao fazer seu primeiro depósito, os novos jogadores recebem um generoso bônus de boas-vindas. Esse bônus aumenta o saldo inicial. Ele fornece os meios para se familiarizar com os jogos.
- Giros grátis.
Algumas promoções incluem rodadas grátis em caça-níqueis populares. Isso dá aos jogadores a chance de experimentar os jogos. Não há necessidade de gastar dinheiro extra.
- Bônus de recarga.
Os bônus de recarga são oferecidos regularmente aos jogadores existentes. Os bônus estão disponíveis quando os jogadores fazem novos depósitos. Essa oferta incentiva a participação contínua no cassino.
- Programa VIP.
Os jogadores regulares podem aproveitar os benefícios exclusivos do programa VIP. Isso inclui gerentes de conta, ofertas personalizadas e outros privilégios especiais.
- Cashback.
O programa de cashback recompensa os jogadores com uma porcentagem de suas perdas. Ele oferece segurança em momentos menos favoráveis.
- Torneios especiais.
Os cassinos on-line realizam regularmente torneios com prêmios atraentes. Os jogadores podem competir entre si. Isso acrescenta um aspecto competitivo à experiência de jogo.
- Bônus de indicação.
Ao indicar amigos para o cassino, os jogadores podem receber bônus especiais. Os bônus ficam disponíveis quando os amigos se cadastram e começam a jogar.
Essas promoções tornam o jogo mais divertido e dão aos jogadores benefícios adicionais.
Suporte ao cliente em cassinos on-line no Brasil
O suporte ao cliente é uma parte importante da experiência de jogar em cassinos on-line no Brasil. Os melhores cassinos oferecem canais eficientes e responsivos. Eles estão disponíveis o tempo todo.
- Bate-papo ao vivo. Oferece interação direta em tempo real. Conveniente para a resolução imediata de problemas.
- E-mail. Útil para perguntas detalhadas ou envio de documentos.
- Telefone. Ideal para aqueles que preferem comunicação verbal.
É muito importante que o suporte também esteja disponível por meio do aplicativo móvel do cassino. Isso garantirá que a ajuda esteja sempre disponível.
Os online cassinos que se concentram na conveniência do usuário geralmente oferecem esses recursos:
- Perguntas frequentes detalhadas. Para esclarecimento rápido de dúvidas comuns.
- Guias de jogos. Ajudam você a entender as regras e os recursos dos jogos.
- Informações bancárias. Explica os processos de depósito e saque.
É importante que o serviço de suporte seja totalmente traduzido para o português. Isso permitirá que os jogadores do Brasil entendam e resolvam problemas sem a barreira do idioma.
Uma visão geral dos cassinos on-line populares no Brasil
Vamos entrar no intrigante universo dos cassinos on-line no Brasil. Em nossa busca por entretenimento de qualidade e jogos de azar emocionantes, analisaremos os cassinos populares que oferecem uma jornada única para os jogadores brasileiros.
Cassino Izzi
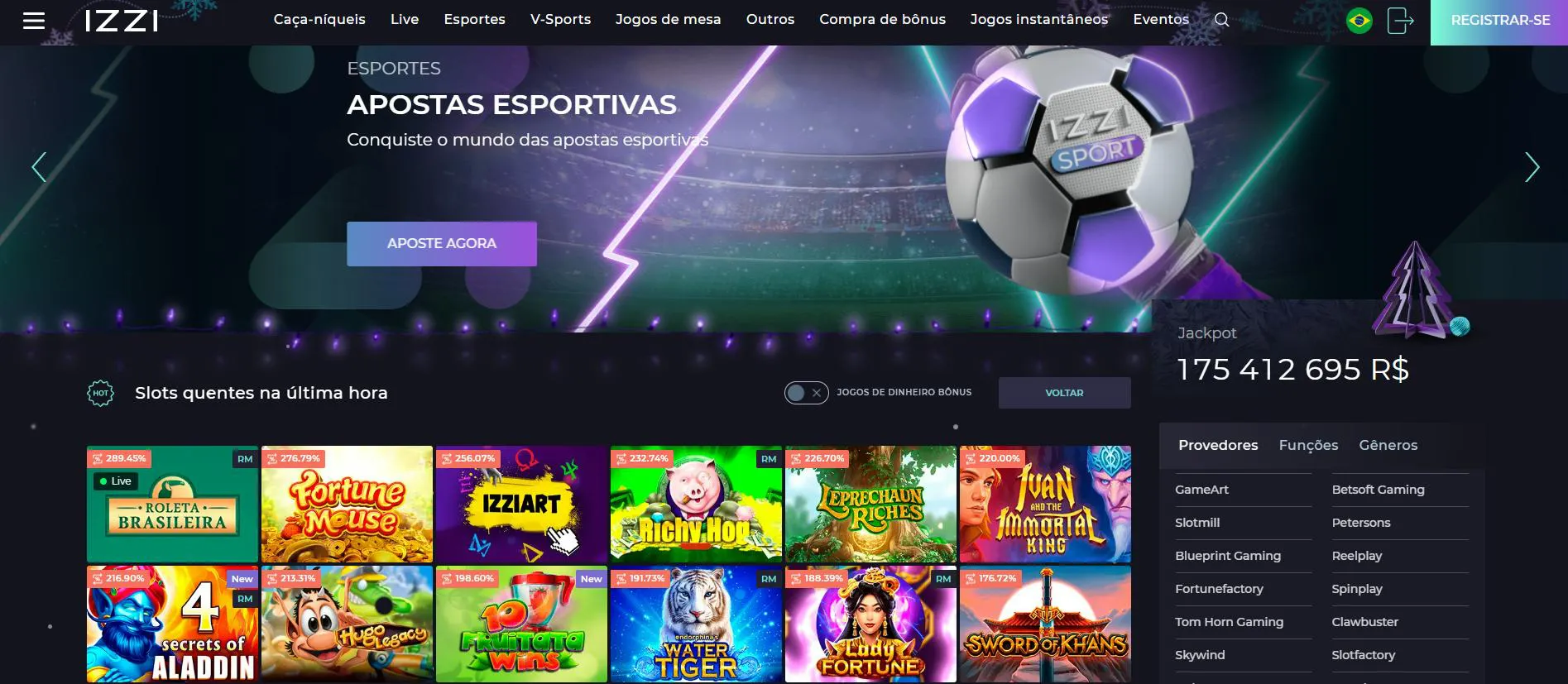
O Izzi Casino entrou no mercado brasileiro com uma oferta inovadora. O cassino online foi fundado em 2022. O Izzi Casino é operado pela Carrer N.V.
O Izzi possui uma impressionante coleção de mais de 5.000 jogos. O cassino é voltado para o mercado brasileiro. Um destaque do cassino é a inclusão da roleta brasileira na seção ao vivo. Ela oferece uma experiência de jogo autêntica em português.
O Izzi Casino oferece mais de 50 provedores, incluindo NetEnt, Playson e Evolution Gaming. O foco principal são os caça-níqueis, que podem ser jogados gratuitamente. A seção de jogos de mesa também é bastante extensa, embora a busca por títulos específicos seja limitada.
O Izzi Casino impressiona com o seu bônus de boas-vindas. Ele vem com 100 por cento até 1.500 euros e 300 rodadas grátis. O programa VIP consiste em quatro níveis. Ele oferece benefícios exclusivos à medida que os jogadores progridem.
A adaptação ao mercado brasileiro se reflete nos métodos de pagamento. Eles incluem Pix, boleto bancário e transferência bancária. O depósito mínimo é de R$ 20 e o máximo é de R$ 10.000. Isso depende do método escolhido.
O cassino opera sob uma licença de Curaçao. O Izzi Casino oferece segurança com o protocolo SSL de 128 bits. O cassino possui medidas de combate à lavagem de dinheiro. O Izzi opera uma verificação de geração de números aleatórios. Isso gera confiança.
O cassino tem um aplicativo para Android e uma versão móvel otimizada. O Izzi Casino oferece flexibilidade aos jogadores. Ele proporciona uma experiência estável em uma variedade de dispositivos.
O Izzi Casino se destaca no cenário brasileiro. Ele oferece uma plataforma envolvente com registro rápido, uma ampla seleção de jogos e suporte em tempo real.
Cassino Spin
O Spin Casino é um cassino on-line. Ele oferece uma experiência excepcional para os jogadores do Brasil. O cassino foi fundado em 2001. O cassino é de propriedade da Bayton Ltd. Ele opera sob uma licença da Malta Gaming Authority (MGA).
O Spin Casino oferece aos usuários mais de 700 jogos. Entre eles estão mais de 500 caça-níqueis, blackjack, roleta, bacará, videopôquer, jogos ao vivo, keno, craps, loterias e raspadinhas. Os jogos são desenvolvidos por fornecedores de software renomados. Entre eles estão a Microgaming e a Evolution Gaming. O cassino se destaca por seus jogos com crupiê ao vivo. Eles são desenvolvidos pela Evolution Gaming.
O Spin Casino oferece aos jogadores um generoso bônus de boas-vindas. Seu valor chega a R$ 5.000 e 75 rodadas grátis. O programa VIP, com diferentes níveis, oferece diversos benefícios. Por exemplo, bônus mensais, promoções exclusivas e um gerente de conta pessoal.
Há uma variedade de métodos de depósito e saque disponíveis. Entre eles estão Visa, Mastercard, Skrill, Neteller, Paysafecard, Lobanet, Pix e outros.
O cassino se caracteriza por um processo de saque eficiente. Geralmente, ele é concluído dentro de 1 a 5 dias úteis.
O atendimento ao cliente é feito por e-mail, chat e telefone. O atendimento ao cliente está disponível em vários idiomas. Isso inclui o português. Isso é importante para atender à diversidade de jogadores. O cassino tem um aplicativo móvel. Ele é compatível com Android, iOS, tablets, Mac/PC. Isso proporciona flexibilidade aos jogadores.
O Spin Casino se destaca não apenas pelo número de jogos, mas também pela qualidade de sua experiência ao vivo e pelos bônus generosos.
Cassino Jackpot City

O Jackpot City Casino oferece uma experiência de jogo emocionante. É um cassino que foi fundado em 1998. É operado pela Digimedia Limited Casinos. Sua ampla oferta de jogos e bônus generosos fazem dele uma escolha popular entre os jogadores brasileiros.
Ao entrar no Jackpot City, os jogadores brasileiros recebem um bônus de boas-vindas empolgante. Ele inclui 10 rodadas grátis no momento do registro e o dobro do seu primeiro depósito de até R$ 500. Esse é um incentivo atraente para explorar a extensa coleção de jogos. A variedade de bônus, incluindo promoções regulares e um programa VIP, agrega valor ao jogo para os jogadores. As ofertas atualizadas com frequência os mantêm interessantes.
O Jackpot City Casino oferece aos jogadores métodos de pagamento convenientes e seguros. Os jogadores podem fazer pagamentos facilmente. Eles podem retirar os ganhos da plataforma usando seus métodos preferidos. O Jackpot City é caracterizado por saques rápidos. A maioria dos pagamentos é processada em 24 a 48 horas. Isso garante uma experiência eficiente para o jogador.
O cassino é licenciado pela Malta Gambling Authority e tem certificação eCOGRA. O Jackpot City prioriza a segurança e a proteção dos jogadores. Ele garante um ambiente de jogo seguro e protegido.
O Jackpot City Casino se orgulha de seu amplo serviço multilíngue. Ele oferece acesso a vários idiomas, inclusive o português. Isso permite que os jogadores aproveitem o jogo e interajam com a plataforma em seu idioma nativo. Isso cria uma experiência de jogo mais confortável e personalizada.
A equipe de suporte ao cliente do Jackpot City está sempre disponível. Os jogadores recebem assistência rápida e eficiente em todos os momentos. Ela está disponível por e-mail, chat e telefone. A equipe de suporte está pronta para responder a perguntas.
O Jackpot City Casino é uma ótima opção para os jogadores brasileiros que procuram uma experiência de jogo completa.
Europa Casino
O Europa Casino foi fundado em 2001. Ele oferece uma experiência empolgante para os jogadores brasileiros. O cassino é operado pela Imperial E-Club Limited Casinos.
O Europa Casino oferece mais de 1.000 jogos. Eles atendem às preferências de todos os jogadores. Estão disponíveis desde emocionantes caça-níqueis e jogos de mesa clássicos até variantes ao vivo. O cassino utiliza a renomada tecnologia Playtech para oferecer uma experiência de jogo de alta qualidade.
A inclusão do português brasileiro entre os idiomas suportados enfatiza o compromisso do Europa Casino em atender aos seus jogadores brasileiros. O suporte ao cliente está disponível por e-mail, chat ao vivo e telefone. Ele é caracterizado pela eficiência.
O Europa Casino oferece métodos de pagamento convenientes. Estes incluem Pix, boleto bancário, cartões de crédito, transferências bancárias e até mesmo criptomoedas. O cassino é licenciado pela Malta Gaming Authority. O cassino garante a segurança dos dados dos jogadores com criptografia avançada.
Os jogadores são recebidos com um generoso bônus de boas-vindas. Ele totaliza até R$ 12.000 em um período de 12 meses. O cassino oferece promoções contínuas, prêmios por indicação e um programa de fidelidade. Isso cria incentivos adicionais para os jogadores.
O Europa Casino se destaca como uma opção confiável e interessante para os amantes de cassino no Brasil.
Betway Casino
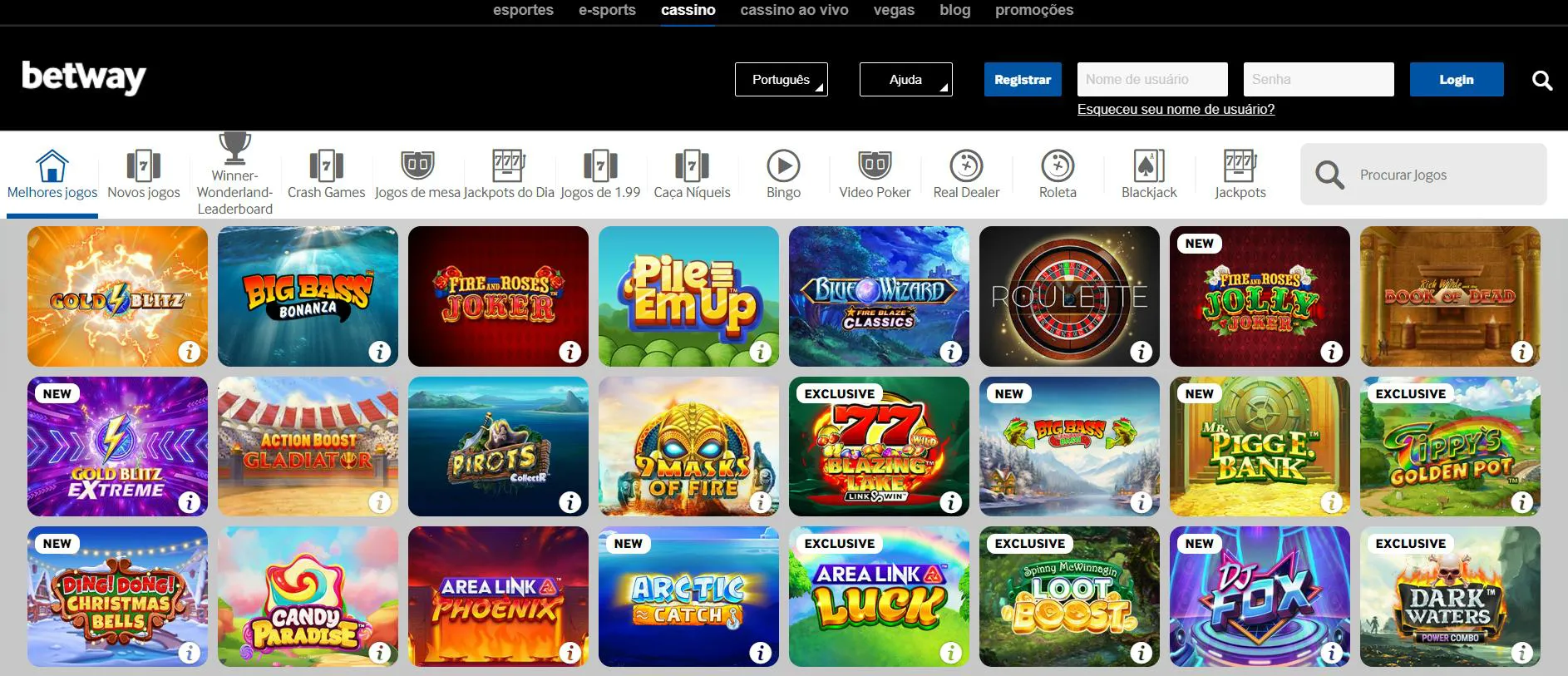
O Betway Casino foi fundado em 2006. Ele é um dos líderes no setor de jogos on-line. Gerenciado pelo Grupo Betway, esse cassino recebe jogadores de todo o mundo.
O cassino tem uma biblioteca impressionante de mais de 400 jogos. Isso permite que o Betway Casino atenda a todos os gostos. Estão disponíveis desde emocionantes caça-níqueis até jogos de mesa clássicos, como blackjack e roleta, e variantes ao vivo. O cassino utiliza a renomada tecnologia da Microgaming, NetEnt e IGT. Isso garante uma experiência de jogo de alta qualidade.
A sala de pôquer do Betway oferece torneios diários. A seção de apostas esportivas amplia a variedade de opções de apostas. Ela inclui transmissão ao vivo.
O Betway Casino oferece suporte em vários idiomas. Entre eles estão o português, o alemão, o grego, o inglês, o espanhol e o finlandês. O suporte ao cliente está disponível por meio de bate-papo ao vivo, telefone e e-mail. Ele se caracteriza por sua eficiência.
O Betway Casino é licenciado pela Comissão de Jogos do Reino Unido e pela Autoridade de Jogos de Malta. A criptografia SSL protege os dados dos jogadores. O Betway Casino tem a marca eCOGRA. Isso garante a segurança e a imparcialidade do jogo.
O bônus de boas-vindas é o destaque. Embora ele seja voltado principalmente para os jogadores de caça-níqueis. O Betway recompensa constantemente os jogadores com promoções semanais. Um clube de recompensas está disponível para eles.
O cassino ao vivo é alimentado pela plataforma Evolution Gaming. Ele oferece uma experiência emocionante ao jogar blackjack, roleta, bacará e outros jogos. O aplicativo móvel e o site otimizado garantem uma experiência perfeita. Eles estão disponíveis para jogadores em dispositivos Android e iOS.
Uma variedade de opções bancárias, incluindo Visa, Mastercard e outras, facilita os depósitos e saques. O Betway Casino se destaca como uma opção confiável e empolgante para os entusiastas de cassino.
Comparação de cassinos populares
Há muitas opções no mundo dos cassinos no Brasil online. Escolher o cassino certo pode ser uma tarefa difícil. Para ajudar nesse processo, preparamos uma tabela comparativa de cinco cassinos on-line populares.
|
Característica |
Betway |
Izzi Casino |
Spin Casino |
Jackpot City Casino |
Europa Casino |
|
🏢 Proprietário |
Betway Group |
Carrer N.V. |
Bayton Ltd |
Digimedia Limited Casinos |
Imperial E-Club Limited Casinos |
|
🗓️ Ano de Estabelecimento |
2006 |
2022 |
2001 |
1998 |
2001 |
|
🎲 Número de Jogos |
400+ |
5,000+ |
700+ |
500+ |
1000 |
|
🎰 Jogos Oferecidos |
Disponível: Slots, Blackjack, Roulette, Baccarat, VideoPoker, LiveGames, Keno, Basketball, Tennis, Football, Horseracing, Scratchcards, Sports |
Disponível: Slots, Blackjack, Roulette, Baccarat, VideoPoker, LiveGames, Keno, Poker |
Disponível: Slots, Blackjack, Roulette, Baccarat, VideoPoker, LiveGames, Bingo, Keno, Craps, Scratchcards |
Disponível: Slots, Blackjack, Roulette, Baccarat, VideoPoker, Jogos ao Vivo, Bingo, Keno, Craps, Cartões de Raspadinha |
Disponível: Slots, Blackjack, Roulette, Baccarat, VideoPoker, LiveGames, Bingo, Keno, Craps, Scratchcards |
|
⚙️ Software Utilizado |
Microgaming, NetEnt, IGT |
NetEnt, Play'n GO, Pragmatic Play, Endorphina e outros |
Microgaming, Evolution Gaming |
Microgaming, NetEnt, Playtech, Crazy Tooth Studio, Foxium, Just For The Win, Rabcat |
Playtech |
|
📱 Dispositivos Compatíveis |
Disponível em Android, iPhone, Windows Phone, Mac / PC, Tablet |
Disponível em Android, iPhone, Mac/PC, Tablet |
Disponível em Android, iPhone, iOS, Mac / PC, Tablet |
Disponível em Android, iPhone, Windows Phone, iPad, Mac / PC, Tablet, Blackberry |
Disponível em Android, iPhone, Windows Phone, iPad, Mac / PC, Tablet, Blackberry |
|
↩️ Velocidade de Pagamento |
1–3 dias |
0–5 dias |
1–5 dias |
1–2 dias |
1–2 dias |
|
💁 Atendimento ao Cliente |
Live chat, Phone |
E-mail, Chat ao Vivo |
E-mail, Chat Ao Vivo, Telefone |
E-mail, Chat Ao Vivo, Telefone |
Email, Chat ao Vivo, Telefone |
Esta tabela o ajudará a fazer escolhas informadas e a aproveitar as oportunidades de jogos emocionantes.
Como escolher um cassino on-line confiável no Brasil
Escolher o cassino on-line certo é fundamental. É importante para uma experiência de jogo segura e agradável. Aqui estão algumas dicas. Elas ajudarão os jogadores brasileiros a escolher um cassino on-line confiável.
- Licença e regulamentação.
Certifique-se de que o cassino tenha uma licença válida. É importante que ele seja regulamentado por um órgão respeitável. Isso garante que o cassino opere de acordo com as normas legais.
- Segurança e privacidade.
Verifique se o site usa tecnologia de criptografia. Isso é importante para proteger as informações do jogador. A privacidade e a segurança dos dados pessoais são fundamentais.
- Variedade de jogos.
Escolha um cassino que ofereça uma variedade de jogos. Isso garante que você terá uma variedade de opções para escolher.
- Fornecedores de software.
Verifique com quais fornecedores de software o cassino está associado. Trabalhar com fornecedores de boa reputação indica qualidade e confiabilidade.
- Bônus e promoções.
Avalie as ofertas de bônus e promoções disponíveis. No entanto, não se esqueça dos termos e condições de apostas.
- Suporte ao cliente.
Certifique-se de que o cassino ofereça um suporte eficaz ao cliente. A disponibilidade de chat ao vivo, e-mail e telefone é importante. Um suporte acessível e rápido é essencial.
- Métodos de pagamento.
Certifique-se de que o cassino ofereça métodos de pagamento seguros e convenientes. Cartões de crédito, transferências bancárias e carteiras digitais são ideais.
- Avaliações e resenhas.
Confira as avaliações e os comentários de outros jogadores. As avaliações reais podem fornecer informações valiosas sobre a confiabilidade de um cassino.
Siga essas recomendações. Você poderá escolher um cassino on-line confiável.
Registro no cassino on-line: passo a passo para jogadores brasileiros

Registrar-se em um cassino on-line é o início de uma jornada emocionante, cheia de diversão e oportunidades de ganhos. Preparamos um guia passo a passo para os jogadores brasileiros. Siga cada passo cuidadosamente. Isso garantirá um registro sem complicações e aproveitará ao máximo a sua experiência de jogo on-line.
- Escolha de um cassino.
Escolha um cassino on-line de boa reputação. Ele deve atender às suas preferências de jogo e oferecer transações seguras.
- Formulário de registro.
Clique no botão «Registrar» no site do cassino escolhido. Preencha o formulário de registro. Forneça informações precisas. Isso inclui nome, data de nascimento, endereço de e-mail e número de telefone.
- Verificação da conta.
Após preencher o formulário, você receberá um e-mail ou SMS com um link ou código. Siga o link. Digite o código. Você precisa disso para verificar sua conta.
- Selecione um método de pagamento.
Vá para a seção de pagamento. Escolha uma forma segura e conveniente de depositar e sacar fundos.
- Bônus de boas-vindas
Verifique se há bônus de boas-vindas disponíveis. Familiarize-se com os termos e condições. Alguns cassinos oferecem rodadas grátis ou bônus em dinheiro no seu primeiro depósito.
- Explore a plataforma
Depois de se registrar, explore a variedade de jogos disponíveis. Os cassinos brasileiros online oferecem tudo, desde caça-níqueis emocionantes até mesas de cassino ao vivo.
Siga estas etapas simples. Você estará pronto para aproveitar a diversão e a emoção que os cassinos on-line têm a oferecer.
Perguntas frequentes
Posso jogar com dinheiro real em cassinos on-line?
Sim, muitos cassinos on-line permitem que os jogadores brasileiros joguem com dinheiro real. Certifique-se de escolher cassinos confiáveis e verifique as opções de pagamento disponíveis.
Que jogos posso encontrar nos cassinos on-line?
Os cassinos on-line oferecem uma grande variedade de jogos. Isso inclui caça-níqueis, blackjack, roleta, pôquer e muito mais. Alguns deles também têm cassinos ao vivo com crupiês reais.
Como posso depositar e sacar dinheiro?
Os métodos de pagamento mais comuns incluem cartões de crédito, transferências bancárias, carteiras bancárias e carteiras digitais, como Neteller e Skrill. Verifique quais métodos estão disponíveis no cassino de sua escolha.
Os cassinos on-line oferecem bônus aos jogadores brasileiros?
Sim, muitos cassinos on-line oferecem bônus de boas-vindas, rodadas grátis e promoções contínuas para jogadores brasileiros. Leia os termos e condições para entender os requisitos de apostas.






